4《数据结构》
文章目录
绪论
- 数据结构:研究非数值计算程序设计中的操作对象,以及这些对象之间的关系和操作
- 数据:客观事物的符号表示,所有输入到计算机并被程序处理的符号总称
- 算法:为了解决某类问题而规定的一串有限长的操作序列
- 算法标准:健壮性、有穷性、可行性、及低存储量
- 节点:实体,有处理能力,类似网络的计算机
- 结点:逻辑,链表中的元素,包括数据域和存储下一个结点地址的指针域
- 数据项:数据结构的最小单位
- 数据元素:数据的基本单位,是数据项的集合
逻辑结构
- 集合:无逻辑关系
- 线性结构:有序数据元素的集合
线性表,数组,栈,队列,串 - 非线性结构:一个结点元素可能有多个直接前趋和多个直接后继
多维数组,广义表,树、图
存储结构【物理结构】
- 顺序存储
- 链式存储
- 索引存储
- 散列存储
顺序和链式存储区别
| 顺序存储 | 链式存储 |
|---|---|
| 数组 | 链表 |
| 数据元素放在地址连续的存储单元中 | 数据元素存储在任意的存储单元里 |
| 数据元素在存储器中的相对位置 | 结点中指针 |
| 逻辑相邻 | 逻辑相邻 |
| 物理相邻 | 物理不一定相邻 |
顺序表和数组区别
| 顺序表 | 数组 |
|---|---|
| 逻辑结构角度 | 物理存储角度 |
| 顺序表 是由数组组成的线性表 |
数组和链表的区别
| 数组 | 链表 |
|---|---|
| 连续内存分配 | 动态内存分配 |
| 在栈上分配内存,自由度小【栈必须连续且固定大小,后进先出的取】 | 在堆上分配内存,自由度大【堆是直接随意存取】 |
| 事先固定数组长度,不支持动态改变数组大小 | 支持动态增加或删除元素 |
| 数组元素增加时,有可能会数组越界;数组元素减少时,会造成内存浪费;数组增删时需要移动其它元素 | 使用malloc或者new来申请内存,不用时使用free或者delete来释放内存 |
| 下标访问,访问效率高 | 访问需要从头遍历,访问效率低 |
| 数组的大小是固定的,所以存在访问越界的风险 | 只要可以申请得到链表空间,链表就无越界风险 |
链表结点概念
- 头结点:在第一个结点之前的结点
- 首元结点:链表存储的第一个结点
- 头指针:链表第一个结点的存储位置
链表为空条件
- 带头结点不为空的单链表:L->next!=NULL
- 带头结点为空的单链表:L->next==NULL
- 不带头结点不为空的单链表:L!=NULL
- 不带头结点为空的单链表:L==NULL
- 带头结点的双循坏链表为空的条件:L->next==L->prior=L
链表文章http://t.csdnimg.cn/dssVK
二叉树
二叉树是一种常见的树状数据结构,它由节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。
特点
- 树形结构:二叉树是一种层次结构,由根节点开始,每个节点可以有零、一个或两个子节点。这种结构使得数据可以以分层的方式进行组织和存储。
- 节点:二叉树的每个节点包含一个数据元素,通常表示某种值或对象,以及指向其左子节点和右子节点的指针(引用)。
- 根节点:树的顶部节点称为根节点。它是整个二叉树的起始点,所有其他节点都通过它连接。
- 叶节点:叶节点是没有子节点的节点,它们位于树的末端。
- 子树:每个节点的左子节点和右子节点都可以看作是一个独立的子树,这些子树也是二叉树。
B树
- 节点排序(节点存储:地址信息+索引+表结构中除了索引外的其他信息)
- 一个节点可以存多个元素,元素也排序
- b树和b+树及其区别? - 知乎用户的回答 - 知乎
https://www.zhihu.com/question/57466414/answer/182514854
B+树【MYSQL索引默认数据结构】
- 拥有B树的特点
- 叶子节点之间有指针
- 非叶子节点上的元素在叶子节点上都冗余了,也就是叶子节点中存储了所有的元素,并且排好顺序。
- 非节点存储:地址信息+索引、叶子节点存储:索引+表结构中除了索引外的其他信息)
B树和B+树区别
| B树 | B+树 |
|---|---|
| key和value都在节点上。并且叶子节点之间没有关系 | 非叶子节点没有存value。叶子节点之间有双向指针,有引用链路。 |
| 因为B树的key和value都存在节点上,因此在查找过程中,可能不用查找的叶子节点就找到了对应的值。 | B+树需要查找到叶子节点,才能获取值 |
冒泡排序
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
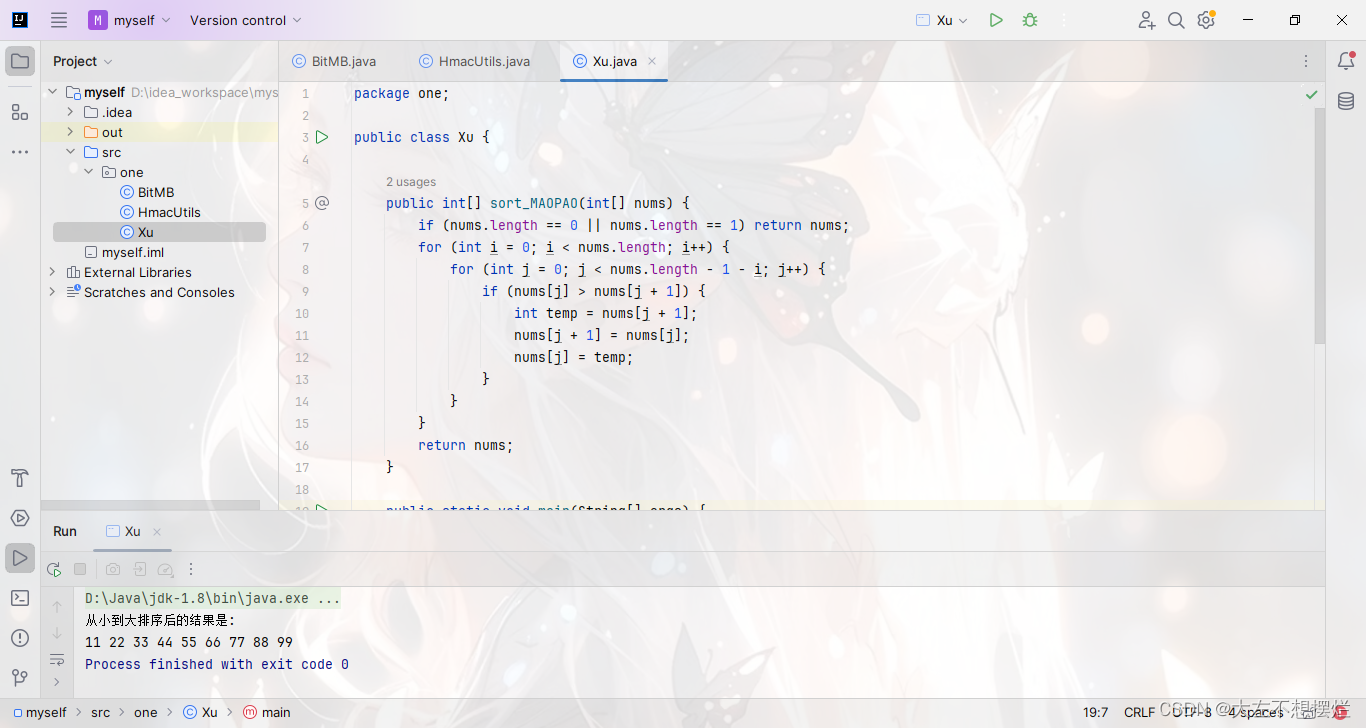
package one;
public class Xu {
public int[] sort_MAOPAO(int[] nums) {
if (nums.length == 0 || nums.length == 1) return nums;
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums.length - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j + 1];
nums[j + 1] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
public static void main(String[] args) {
Xu xu = new Xu();
int[] array = {11, 33, 44, 22, 55, 99, 88, 66, 77};
System.out.println("从小到大排序后的结果是:");
for(int i=0;i<xu.sort_MAOPAO(array).length;i++)
System.out.print(xu.sort_MAOPAO(array)[i]+" ");
}
}
插排
- 1.从第一个元素开始,该元素可以认为已经被排序;
- 2.取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 3.如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 5.将新元素插入到该位置后;
- 6.重复步骤2~5。
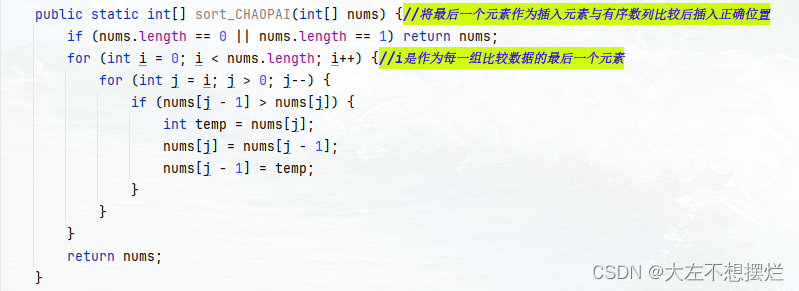
public static int[] sort_CHAOPAI(int[] nums) {//将最后一个元素作为插入元素与有序数列比较后插入正确位置
if (nums.length == 0 || nums.length == 1) return nums;
for (int i = 0; i < nums.length; i++) {//i是作为每一组比较数据的最后一个元素
for (int j = i; j > 0; j--) {
if (nums[j - 1] > nums[j]) {
int temp = nums[j];
nums[j] = nums[j - 1];
nums[j - 1] = temp;
}
}
}
return nums;
}
选排
1.首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2.再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3.重复第二步,直到所有元素均排序完毕。
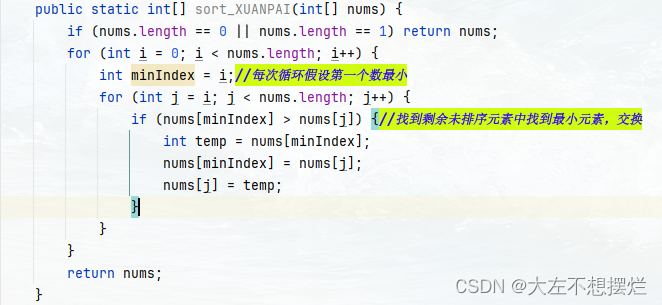
public static int[] sort_XUANPAI(int[] nums) {
if (nums.length == 0 || nums.length == 1) return nums;
for (int i = 0; i < nums.length; i++) {
int minIndex = i;//每次循环假设第一个数最小
for (int j = i; j < nums.length; j++) {
if (nums[minIndex] > nums[j]) {//找到剩余未排序元素中找到最小元素,交换
int temp = nums[minIndex];
nums[minIndex] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
快排
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序
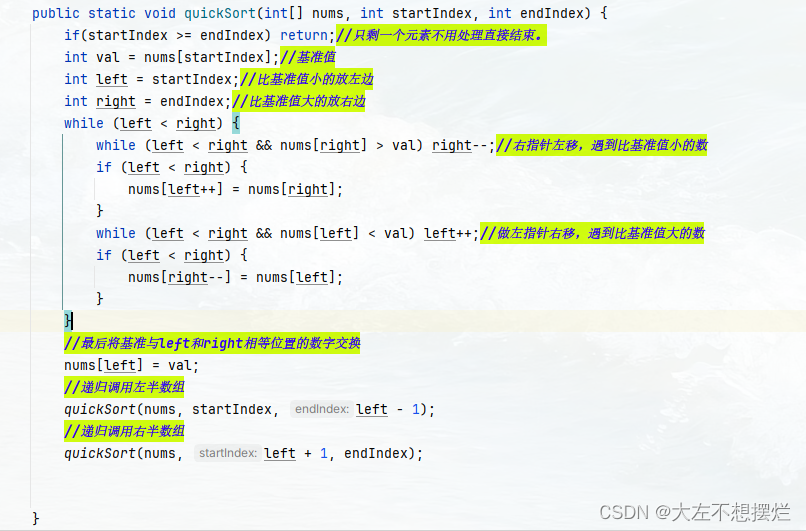
public static void quickSort(int[] nums, int startIndex, int endIndex) {
if(startIndex >= endIndex){//只剩一个元素不用处理直接结束。
return;
}
int val = nums[startIndex];//基准值
int left = startIndex;//比基准值小的放左边
int right = endIndex;//比基准值大的放右边
while (left < right) {
while (left < right && nums[right] > val) right--;//右指针左移,遇到比基准值小的数
if (left < right) {
nums[left++] = nums[right];
}
while (left < right && nums[left] < val) left++;//做左指针右移,遇到比基准值大的数
if (left < right) {
nums[right--] = nums[left];
}
}
//最后将基准与left和right相等位置的数字交换
nums[left] = val;
//递归调用左半数组
quickSort(nums, startIndex, left - 1);
//递归调用右半数组
quickSort(nums, left + 1, endIndex);
}
public static void main (String[]args){
Random rd = new Random();
int[] num = new int[10];
for (int i = 0; i < num.length; i++) {
num[i] = rd.nextInt(100) + 1;
}
System.out.println(Arrays.toString(num));
quickSort(num,0,num.length-1);
System.out.println(Arrays.toString(num));
// for (int i = 0; i < xu.sort_MAOPAO(array).length; i++)
// System.out.print(xu.sort_MAOPAO(array)[i] + " ");
}