矩阵可对角化的充要条件及证明

我的小程序：

对角化：若方阵A相似于对角矩阵，即存在可逆矩阵P和对角矩阵D，有 $A = PDP^{-1}$ ，则称A可对角化。

可对角化的充要条件：

n*n阶矩阵A可对角化的充分必要条件是矩阵A有n个线性无关的特征向量。

充分性证明：

设A的n个线性无关的特征向量为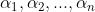 $\alpha _{1},\alpha _{2},...,\alpha _{n}$ ，对应的特征值为 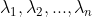$\lambda _{1},\lambda _{2},...,\lambda _{n}$ ，特征向量构成矩阵P=[ 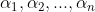$\alpha _{1},\alpha _{2},...,\alpha _{n}$ ].则：

$AP = A[\alpha _{1},\alpha _{2},...,\alpha _{n}] = [A\alpha _{1},A\alpha _{2},...,A\alpha _{n}] = [\lambda _{1}\alpha _{1},\lambda _{2}\alpha _{2},...,\lambda _{n}\alpha _{n}] = [\alpha _{1},\alpha _{2},...,\alpha _{n}]\begin{bmatrix} \lambda _{1} & 0 & . & . & 0\\ 0 & \lambda _{2} & . & . & .\\ . & .& . & . &. \\ .& . & . & . &0 \\ 0& . & . & 0& \lambda _{n} \end{bmatrix} = P\begin{bmatrix} \lambda _{1} & 0 & . & . & 0\\ 0 & \lambda _{2} & . & . & .\\ . & .& . & . &. \\ .& . & . & . &0 \\ 0& . & . & 0& \lambda _{n} \end{bmatrix}$

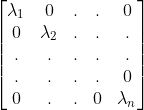将对角矩阵 $\begin{bmatrix} \lambda _{1} & 0 & . & . & 0\\ 0 & \lambda _{2} & . & . & .\\ . & .& . & . &. \\ .& . & . & . &0 \\ 0& . & . & 0& \lambda _{n} \end{bmatrix}$ 记为D，则上式可化简为AP = PD。因为n个特征向量线性无关，所以P=[ 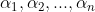$\alpha _{1},\alpha _{2},...,\alpha _{n}$ ]可逆，所以 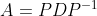$A = PDP^{-1}$ ，即A可对角化。

必要性证明：

A可对角化，即 $A = PDP^{-1}$ ，可得AP = PD.

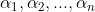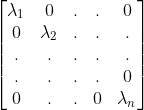设P的列元素为 $\alpha _{1},\alpha _{2},...,\alpha _{n}$ ，即P=[ $\alpha _{1},\alpha _{2},...,\alpha _{n}$ ]，设对角矩阵D为 $\begin{bmatrix} \lambda _{1} & 0 & . & . & 0\\ 0 & \lambda _{2} & . & . & .\\ . & .& . & . &. \\ .& . & . & . &0 \\ 0& . & . & 0& \lambda _{n} \end{bmatrix}$ .

则：

；

$PD = [\alpha _{1},\alpha _{2},...,\alpha _{n}]\begin{bmatrix} \lambda _{1} & 0 & . & . & 0\\ 0 & \lambda _{2} & . & . & .\\ . & .& . & . &. \\ .& . & . & . &0 \\ 0& . & . & 0& \lambda _{n} \end{bmatrix}= [\lambda _{1}\alpha _{1},\lambda _{2}\alpha _{2},...,\lambda _{n}\alpha _{n}]$ ；

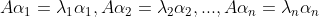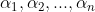由AP = PD得： $A\alpha _{1} = \lambda _{1}\alpha _{1},A\alpha _{2} = \lambda _{2}\alpha _{2},...,A\alpha _{n} = \lambda _{n}\alpha _{n}$ .因为P可逆，显然 $\alpha _{1},\alpha _{2},...,\alpha _{n}$ 都不为0，所以 $\lambda _{1},\lambda _{2},...,\lambda _{n}$ 是A的特征值， $\alpha _{1},\alpha _{2},...,\alpha _{n}$ 是A的特征向量且线性无关。得证。

参考资料：David.C.Lay《线性代数及其应用》

我的​​​​​​​小程序：

我的小程序：