lecture 5 ： policy gradient introduction

lecture 5 ： policy gradient introduction

求 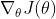$\nabla_{\theta} J(\theta)$ 时运用了如下一个技巧：

于是，

由于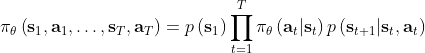 $\pi_{\theta}\left(\mathbf{s}_{1}, \mathbf{a}_{1}, \ldots, \mathbf{s}_{T}, \mathbf{a}_{T}\right)=p\left(\mathbf{s}_{1}\right) \prod_{t=1}^{T} \pi_{\theta}\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right) p\left(\mathbf{s}_{t+1} | \mathbf{s}_{t}, \mathbf{a}_{t}\right)$ 则 $\nabla_{\theta} J(\theta)$ 变为：

$\nabla_{\theta} J(\theta)=E_{\tau \sim \pi_{\theta}(\tau)}\left[\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right)\right]$

在代码实现的时候，用trajactory的平均来估计 $\nabla_{\theta} J(\theta)$ ，即：

接下来又分析了 vanila policy gradient 方法的 high varience ：

直观上的理解就是，某个概率分布（如图中的r(r), 受数据的偏移影响较大）

为了减少varience, 开始如下分析：

由于某个时刻 前面的reward 对现在时刻的微分没有影响，所以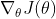 $\nabla_{\theta} J(\theta)$ 变为：

之后又加了baseline，如下所示：

b 可以取任何值(不依赖于cita) , 为什么要减？因为要减少varience （计算方差的公式前面的平方项的效果不后面那一项大)

减去b 之后，有无影响？没有（也可以认为是 unbiased 的项) ，因为：

/******************************************************************************************************************/

课程中也讨论了， b 该取何值？从计算方差的定义出发：

后面那一项，与没有减之前相等，所以消去，前一项对b 求偏导得：

直观的理解就是 weighted expeted reward, weight 由 gradient 决定。

/******************************************************************************************************************/

以上policy gradient 是 on-policy 方法，即由 pilicy 运行产生的data 进行训练，所以此时的方法是data inefficient 的因为它用过一个数据之后就把它丢弃了。一个解决方法是 off-policy的 policy gradient 方法： important sampling: 通过其他的分布来估计现有分布的值。

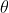可以看到 $\theta^{\prime}\right$ 的微分由 $\theta$ 的分布决定。至此，算法变为了off-policy, 即通过不是该策略产生的数据来训练参数。通过等式可以看出，要通过importance ratio 进行调整。其中：

之后介绍了一种简化expotial 的方法

课程最后介绍了使用important sampling 的例子，如 locomotion imitation , 从现实中的人类行走这个分布抽取数据。